The Istanbul Technical University Method
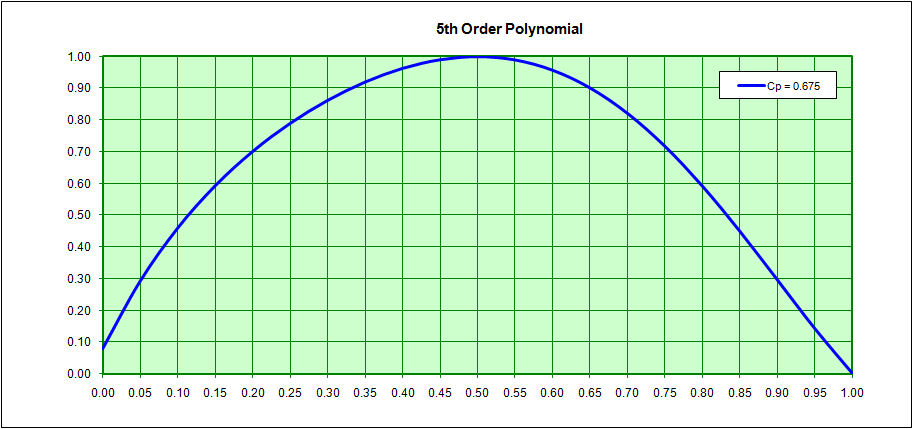
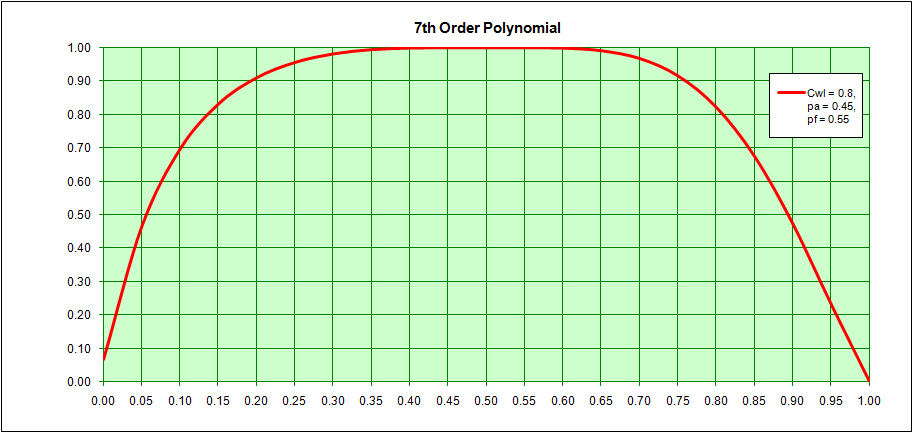
Here is another method, that I believe is from the Istanbul Technical University, in which a ship's entire waterline or sectional area curve can be treated as a single 5th order polynomial for ship's with no parallel midbody or as a 7th order polynomial for ships with parallel midbody.
Specifically, for waterlines and sectional area curves without parallel midbody;
y = a + bx + cx^2 + dx^3 +ex^4 + fx^5
Where x = 0 is the transom and x = 1 is the bow
Here, for the sectional area curve, the boundary conditions are;
- @ x = 0, y = the Transom Area Coefficient (At/Ax)
- @ x = 1, y = 0 (assuming the ship does not have a bulbous bow)
- @ x = 0.5, y = 1 (assuming that the midship section is equal to the section of max area)
- @ x = 0.5, y' = 0 (as above)
- S y dx = Cp
- S yx dx = Cp ( 0.5 - LCB / 100 )
For the Design Waterline, these boundary conditions are;
- @ x = 0, y = the Transom Beam Coefficient (Bt/Bx)
- @ x = 1, y = 0 (assuming the ship does not have a bulbous bow)
- @ x = 0.5, y = 1 (assuming that the midship section is equal to the section of max beam)
- @ x = 0.5, y' = 0 (as above)
- S y dx = Cwl
- S yx dx = Cwl ( 0.5 - LCF / 100 )
For ships with parallel midbody
y = a + bx + cx^2 + dx^3 +ex^4 + fx^5 + gx^6 + hx^7
Here, for the sectional area curve, two additional points are defined as
pf = the forward extent of the parallel midbody
pa = the aft extent of the parallel midbody
The boundary conditions are;
- @ x = 0, y = the Transom Area Coefficient (At/Ax)
- @ x = 1, y = 0 (assuming the ship does not have a bulbous bow)
- @ x = pf, y = 1 (assuming that throughout the extent of the parallel midbody sectional area = maximum area)
- @ x = pa, y = 1 (as above)
- @ x = pf, y' = 0 (as above)
- @ x = pa, y' = 0 (as above)
- S y dx = Cp
- S yx dx = Cp ( 0.5 - LCB / 100 )
For the Design Waterline, these boundary conditions are;
- @ x = 0, y = the Transom Beam Coefficient (Bt/Bx)
- @ x = 1, y = 0 (assuming the ship does not have a bulbous bow)
- @ x = pf, y = 1 (assuming that throughout the extent of the parallel midbody sectional area = max beam)
- @ x = pa, y = 1 (as above)
- @ x = pf, y' = 0 (as above)
- @ x = pa, y' = 0 (as above)
- S y dx = Cwl
- S yx dx = Cwl ( 0.5 - LCF / 100 )
Using the Matrix ("Array") capabilities of a Spreadsheet Program like Excel it is fairly easy to solve for the coefficients in the original polynomials.
A sample of the 5th order and 7th order polynomials is shown below.